Enterprise Service Bus in Python

Also available in Català, Deutsch, Français, Italiano, Português, and 한국어.
Let's start with a question, what is an ESB? But even prior to that, what does ESB stand for? And SOA? These acronyms can be a source of confusion, indeed.
ESB expands to an Enterprise Service Bus. SOA stands for Service Oriented Architecture.
That still doesn't explain too much so here's more information in plain English, without too much of corporate speak.
Think what happens when you log in to your bank's app:
- Your name is displayed
- The account balance is there
- Your credit and debit cards are shown
- A list of your mutual funds can be there
- You get a pre-computed list of attractive loans you might be interested in
Now, it's very likely that all these pieces belong to different systems and applications, each of which exposes data through an interface of some sort (REST, SOAP, Kafka, SFTP, CSV, doesn't really matter):
- No. 1 is from a CRM running on Linux and Oracle
- No. 2 is from a COBOL system on z/OS mainframe
- No. 3 is said to be from a mainframe but they're too tight-lipped to tell you anything, only that they prefer CSV over anything else
- No. 4 is from a mix of PHP and JavaScript running on Windows
- No. 5 is from PostgreSQL, Python and Java running on Linux and IBM System i
The question now is, how do you make the frontend app talk to 1-5? Well, you don't.
This is the fundamental basis of making sure such environments can scale above a handful of systems. You don't let them talk to each other directly.
In the diagram below, each invocation of a service another system offers is represented in a line of different width or style:
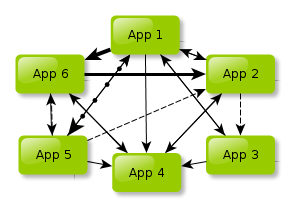
Note that we didn't even show you any higher-level processes (App1 invokes App2 and either App3 or App5 depending on whether an earlier response from App 6 was successful so that App4 can at a later time grab data produced by App 2 but only if App 1 doesn't forbid it etc.).
Also note that we're not talking about servers - each of the systems may run on 10 physical servers so there will be at least 60 physical components talking to each other.
Still, some questions become apparent.
How to separate interfaces? How can you plan roll-outs? How do you coordinate updates or planned downtimes if each application is managed by different teams, vendors or departments and half of the original developers have left already?
If you think you can handle 6 applications, how about 30 of them?
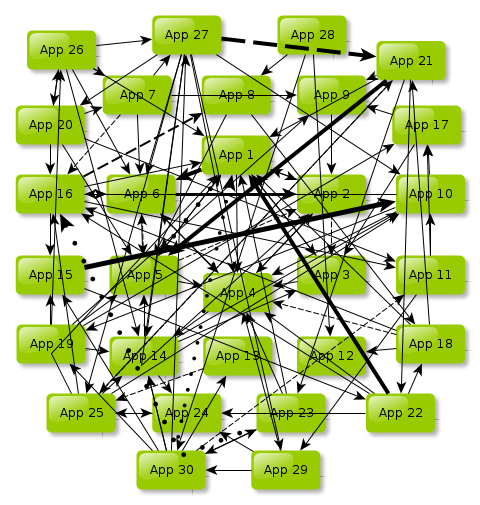
Can you deal with 400? How about 2000? Each application can be a unique ecosystem requiring 10 servers or other devices to run on, so this is 20k moving parts spread over continents and all sort of technical or cultural boundaries, all that parts constantly and incessantly wishing to exchange messages and to chatter with each other all the time without any let-up, ever. (We’ll spare you a diagram)
There's a good name for that situation. It's called a mess.
How can you clean up the mess?
First thing is to honestly admit that the situation has gotten out of hand. This allows one to look for a remedy without feeling too much guilt. OK, it happened, you didn't know any better, but there's a chance it can be cleaned up.
This may mean an organizational change in an approach to IT but another step is to recall that systems and applications are not created merely to push data around. They're meant to support business processes, regardless of what your business is, banking, audio recordings, radio devices, anything.
Once you got these two clearly stated you can start thinking of building or redesigning your systems around services.
A service is something interesting, reusable and atomic that is offered by one system to other applications willing to make a good use of it, but it's never exposed directly in a point-to-point manner. This is the shortest meaningful definition possible.
Does a given piece of functionality of a system fulfill these 3 requirements?
▸ I for Interesting
▸ R for Reusable
▸ A for Atomic
If yes, then there's a very good chance it could and should be exposed as a service to other systems, though never directly.
Let's discuss this IRA approach through a couple of examples.
| Variable | Notes |
|---|---|
| Environment | An utility company's CRM |
| Functionality | Returning a list of customers that were active in a self-service portal in Q3 2021 |
| Is it interesting? | Yes, quite interesting. This can be used to generate all sorts of useful reports and statistics. |
| Is it reusable? | No, not really. Although it does allow for creating higher-level constructs, such as statistics for a whole year, it's clear that there won't be much need for it in 2028. |
| Is it atomic? | Most likely, yes. If there are similar services for other quarters, it will be possible to get an insight into the whole year |
| How to make it IRA? | 1) Make it accept arbitrary start and stop dates instead of being limited to one quarter only. 2) Make it accept arbitrary applications, not only the portal, let the application you're interested in be an input parameter, it cannot be hard-coded to the portal only |
| Variable | Notes |
|---|---|
| Environment | e-commerce site |
| Functionality | Returning each piece of information ever collected regarding a given customer |
| Is it interesting? | Well, yes. If you have access to the whole of it you'll be always able to choose what you really need. |
| Is it reusable? | Funnily enough, not exactly. There will be very few applications, if any, that will be interested in each and every bit of data. |
| Is it atomic? | Definitely not. This monster functionality is bound to be logically composed of dozens of smaller parts. |
| How to make it IRA? | 1) Split it into smaller pieces. Think what describes a customer - they have their addresses, phones, favorite products, contact methods they prefer and so on - each of these should be turned into an independent service. 2) Use ESB to create composite services out of the atomic ones |
| Variable | Notes |
|---|---|
| Environment | Any CRM anywhere |
| Functionality | Updating column CUST_AR_ZN in table C_NAZ_AJ after someone creates an account |
| Is it interesting? | Absolutely not. This is a CRM's internal function. No one in the sane world wants to deal with such low-level functionality. |
| Is it reusable? | Yes, probably. An account can be created through multiple channels so this seems something reusable. |
| Is it atomic? | Seems so, yes. It's just a simple update of one column in one table. |
| How to make it IRA? | Don't even attempt to turn it into a service. It is not interesting. No one wants to think of particular columns and tables in one system. This is a CRM's intricate detail, so even though it is reusable and atomic, you must not offer a service on top of it. It is your, the CRM's, responsibility to think of it, don't make anyone else shoulder it as well. |
| Variable | Notes |
|---|---|
| Environment | A mobile telecommunication operator |
| Functionality | Refilling a prepaid card in a billing system |
| Is it interesting? | Extremely so. Everyone wants to use it, through text messages, IVR, chats, portals, gift cards etc. |
| Is it reusable? | Very reusable, it can take part in all sort of higher-level processes |
| Is it atomic? | Yes, from the calling application's point of view, it can either refill a card or not. That a billing system will implement this functionality as a series of steps is irrelevant. From a business perspective it's an atomic, indivisible service offered by a billing system. |
| How to make it IRA? | It already is IRA. |
If you've done any programming in the last 50 or so years it is now very clear that exposing a service is precisely like exposing an API in one part of code to another. The only difference is that you're not dealing with sub-modules of a single system, you're operating on a level of an entire environment of disparate systems.
Making services available on an ESB in an SOA
Now that you know that systems don't exchange information directly and you understand what a service is, you can start making use of an ESB.
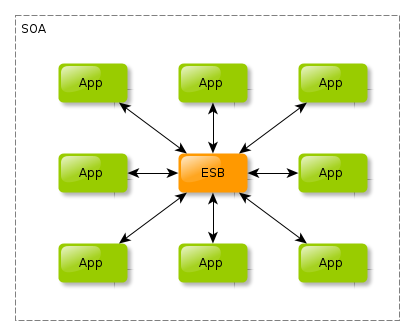
It now becomes the job of ESB to expose and invoke services of the integrated systems. That way, in most cases, only one access method, one interface, needs to be defined between each system and the ESB.
So if, like in the diagram above, you have 8 systems, there will be 16 interfaces (one in each direction) to create, maintain, manage and take care of.
Without an ESB you'd have 56 interfaces to think of and deal with (assuming each systems system talks with each other).
40 interfaces less means less time wasted and more money saved. That's one of the reasons why your Fridays will be less strained.
This fact alone should make you strongly consider introducing an ESB.
If a system undergoes a rewrite, change of ownership, gets split between departments or vendors, it will be a duty of ESB folk to conform with the change. None of the other systems will even notice it because their interface with ESB will be left intact.
When you start breathe IRA services on a daily basis you can begin to think of composite ones.
Remember the 'give-me-everything-you-can-about-that-customer' kind of service above?
It wasn't a good idea to create it but you will sometimes have to deal with client applications that need aggregated and summarized information. It will be ESB people who will be responsible for picking the best atomic services to build a composite one for that particular client system requiring this particular set of composite data.
With time the whole organization will begin to understand that it's no more about database tables, files, batches, functions, routines or records. This will be about an architecture centered on interesting, reusable and atomic services applications offer to ESB.
No longer will people think that applications and system send things over one to another. They will see ESB as a universal access gate to interesting services their own systems can make use of. And they won't even bother with checking who exactly provides what, their systems will only deal with ESB.
It takes time, patience and coordinated effort but it is doable.
But watch out for...
The best way to ruin the whole concept of SOA is to roll out an ESB and expect that matters will smooth out themselves. While still being a terrific idea, simply installing an ESB won't achieve that much, unfortunately.
In the best case, sweeping something under the carpet, like in the diagram below, will achieve nothing.
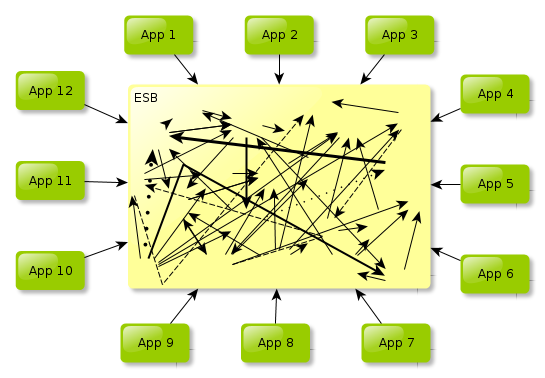
Your IT people will loathe the system and the management will first tolerate an ESB as a new kid on the block but later on it will become a laughing stock. "What, that new silver bullet? Hahaha".
Such consequences are inevitable if an ESB is not part of a bigger plan of actually moving things forward.
An ESB is for banks and similar only, then?
Not at all, no. It is a good choice in any situation requiring multiple data sources and multiple access methods to co-operate in order to achieve an interesting result.
For instance, grabbing latest readings from thermal sensors and publishing it into several channels, like e-mail alerts and an IPhone app does sound like a good fit for an integration platform.
Periodically consulting and monitoring whether all instances of a critical application are all up and if any is not, running a pre-configured script while sending a text message to admins also sounds just fine.
Everything that needs integration in a clear, well-defined environment is possibly a good fit for an ESB service but as always, deciding whether something really is a dream fit will follow from one's experience. Naturally, Zato's authors can help.
But I heard SOA was all about XML, SOAP and web services
Yes, this is what certain people would like you to believe.
If people or vendors you worked with did things such as BASE64-encoding a CSV file and sending it over to you in a SAML2-secured SOAP message then it's quite understandable how you might've developed such an impression.
XML, SOAP and web services have their uses but like anything, they can be misused.
SOA is about a clean and manageable architecture. That a particular service might use SOAP or not is pretty much irrelevant. As an architectural approach, SOA will still be valid even if no SOAP service will be used at all.
If an architect designs a beautiful building, they can't really do much about the color of the paint people choose for the interiors.
So no, SOA is not much about XML, SOAP and web services. These can be used too but it's not the whole story behind it.
You are encouraged to kindly direct your strayed colleagues to this article to make them understand what SOA really is about.
And there's more
This chapter covers only the very basics but should still give you a strong understanding how ESB and SOA should look like and what is needed to achieve a success.
Other topics, not covered here, include, but are not limited to:
- How to get support from the management for an ESB
- How to gather SOA architects and analytical teams
- Introducing a Canonical Data Model (CDM) in an organization
- Key Performance Indicators (KPI) - now that you have a common and unified method of providing services across systems, you should start to monitor and evaluate what is really delivered to you
- Business Process Management (BPM) - how and when to choose a BPM platform to orchestrate the services (answer - not too soon, get yourself familiar with how to build nice and adorable services first)
- What to do with systems that have no APIs? E.g. should an ESB access their databases directly (answer - it depends, there's no golden rule)
So what is Zato exactly?
Zato is an ESB and application server written in Python and can be used for building middleware and backend systems. It is open-source software with commercial and community support available. And Python is a programming language famous for its ease of use and productivity.
Using Python and Zato means you are more productive and need to spend less time on nuisances.
Zato was written by pragmatists for pragmatists. It's not yet another system quickly stitched together by a vendor on the wave of ESB/SOA hype.
In fact, it was born out of practical experience in putting out fires caused by such systems. Indeed, Zato authors spent so much time on dealing with such horror environments that they became virtually immune to any fires.
This is the forge out of which Zato came into existence and that's why it can offer productivity and ease of use unparalleled by other seemingly similar solutions.




 — John Adams
— John Adams